From: http://www-theory.chem.washington.edu/~trstedl/quantum/quantum.html

     This page is intended to give an ordinary person a brief overview of the importance and wonder of quantum mechanics. Unfortunately, most people believe you need the mind of Einstein in order to understand QM so they give up on it entirely. (Interesting side note: Einstein didn't believe QM was a correct theory!) Even some chemists fall into that category-- to represent physical chemistry our departmental T-shirts have a picture of the below atom, which is almost a century out of date. <Sigh>
     So please read on, and take a dip in an ocean of information that I find completely invigorating!

If the above picture is your idea of an atom, with electrons looping around the nucleus, you are about 70 years out of date. It's time to open your eyes to the modern world of quantum mechanics! The picture below shows some plots of where you would most likely find an electron in a hydrogen atom (the nucleus is at the center of each plot).

What is quantum mechanics?

Simply put, quantum mechanics is the study of matter and radiation at an atomic level.

Why was quantum mechanics developed?

In the early 20th century some experiments produced results which could not be explained by classical physics (the science developed by Galileo Galilei, Isaac Newton, etc.). For instance, it was well known that electrons orbited the nucleus of an atom. However, if they did so in a manner which resembled the planets orbiting the sun, classical physics predicted that the electrons would spiral in and crash into the nucleus within a fraction of a second. Obviously that doesn't happen, or life as we know it would not exist. (Chemistry depends upon the interaction of the electrons in atoms, and life depends upon chemistry). That incorrect prediction, along with some other experiments that classical physics could not explain, showed scientists that something new was needed to explain science at the atomic level.

If classical physics is wrong, why do we still use it?

Classical physics is a flawed theory, but it is only dramatically flawed when dealing with the very small (atomic size, where quantum mechanics is used) or the very fast (near the speed of light, where relativity takes over). For everyday things, which are much larger than atoms and much slower than the speed of light, classical physics does an excellent job. Plus, it is much easier to use than either quantum mechanics or relativity (each of which require an extensive amount of math).

What is the importance of quantum mechanics?

The following are among the most important things which quantum mechanics can describe while classical physics cannot:

• Discreteness of energy
• The wave-particle duality of light and matter
• Quantum tunneling
• The Heisenberg uncertainty principle
• Spin of a particle

Discreteness of energy

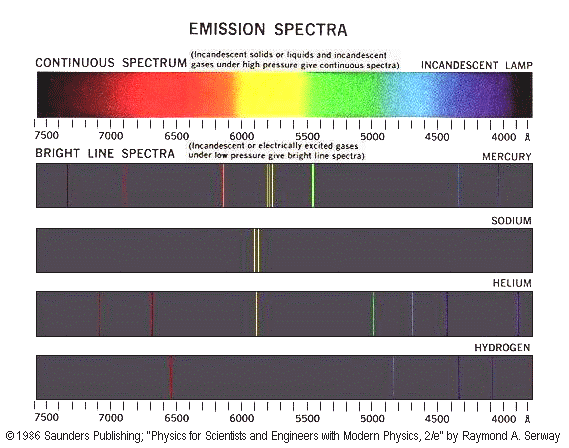
If you look at the spectrum of light emitted by energetic atoms (such as the orange-yellow light from sodium vapor street lights, or the blue-white light from mercury vapor lamps) you will notice that it is composed of individual lines of different colors. These lines represent the discrete energy levels of the electrons in those excited atoms. When an electron in a high energy state jumps down to a lower one, the atom emits a photon of light which corresponds to the exact energy difference of those two levels (conservation of energy). The bigger the energy difference, the more energetic the photon will be, and the closer its color will be to the violet end of the spectrum. If electrons were not restricted to discrete energy levels, the spectrum from an excited atom would be a continuous spread of colors from red to violet with no individual lines.

The concept of discrete energy levels can be demonstrated with a 3-way light bulb. A 40/75/115 watt bulb can only shine light at those three wattage's, and when you switch from one setting to the next, the power immediately jumps to the new setting instead of just gradually increasing.

It is the fact that electrons can only exist at discrete energy levels which prevents them from spiraling into the nucleus, as classical physics predicts. And it is this quantization of energy, along with some other atomic properties that are quantized, which gives quantum mechanics its name.

The wave-particle duality of light and matter

In 1690 Christiaan Huygens theorized that light was composed of waves, while in 1704 Isaac Newton explained that light was made of tiny particles. Experiments supported each of their theories. However, neither a completely-particle theory nor a completely-wave theory could explain all of the phenomena associated with light! So scientists began to think of light as both a particle and a wave. In 1923 Louis de Broglie hypothesized that a material particle could also exhibit wavelike properties, and in 1927 it was shown (by Davisson and Germer) that electrons can indeed behave like waves.

How can something be both a particle and a wave at the same time? For one thing, it is incorrect to think of light as a stream of particles moving up and down in a wavelike manner. Actually, light and matter exist as particles; what behaves like a wave is the probability of where that particle will be. The reason light sometimes appears to act as a wave is because we are noticing the accumulation of many of the light particles distributed over the probabilities of where each particle could be.

For instance, suppose we had a dart-throwing machine that had a 5% chance of hitting the bulls-eye and a 95% chance of hitting the outer ring and no chance of hitting any other place on the dart board. Now, suppose we let the machine throw 100 darts, keeping all of them stuck in the board. We can see each individual dart (so we know they behave like a particle) but we can also see a pattern on the board of a large ring of darts surrounding a small cluster in the middle. This pattern is the accumulation of the individual darts over the probabilities of where each dart could have landed, and represents the 'wavelike' behavior of the darts. Get it?

Quantum tunneling

This is one of the most interesting phenomena to arise from quantum mechanics; without it computer chips would not exist, and a 'personal' computer would probably take up an entire room. As stated above, a wave determines the probability of where a particle will be. When that probability wave encounters an energy barrier most of the wave will be reflected back, but a small portion of it will 'leak' into the barrier. If the barrier is small enough, the wave that leaked through will continue on the other side of it. Even though the particle doesn't have enough energy to get over the barrier, there is still a small probability that it can 'tunnel' through it!

Let's say you are throwing a rubber ball against a wall. You know you don't have enough energy to throw it through the wall, so you always expect it to bounce back. Quantum mechanics, however, says that there is a small probability that the ball could go right through the wall (without damaging the wall) and continue its flight on the other side! With something as large as a rubber ball, though, that probability is so small that you could throw the ball for billions of years and never see it go through the wall. But with something as tiny as an electron, tunneling is an everyday occurrence.

On the flip side of tunneling, when a particle encounters a drop in energy there is a small probability that it will be reflected. In other words, if you were rolling a marble off a flat level table, there is a small chance that when the marble reached the edge it would bounce back instead of dropping to the floor! Again, for something as large as a marble you'll probably never see something like that happen, but for photons (the massless particles of light) it is a very real occurrence.

The Heisenberg uncertainty principle

People are familiar with measuring things in the macroscopic world around them. Someone pulls out a tape measure and determines the length of a table. A state trooper aims his radar gun at a car and knows what direction the car is traveling, as well as how fast. They get the information they want and don't worry whether the measurement itself has changed what they were measuring. After all, what would be the sense in determining that a table is 80 cm long if the very act of measuring it changed its length!

At the atomic scale of quantum mechanics, however, measurement becomes a very delicate process. Let's say you want to find out where an electron is and where it is going (that trooper has a feeling that any electron he catches will be going faster than the local speed limit). How would you do it? Get a super high powered magnifier and look for it? The very act of looking depends upon light, which is made of photons, and these photons could have enough momentum that once they hit the electron they would change its course! It's like rolling the cue ball across a billiard table and trying to discover where it is going by bouncing the 8-ball off of it; by making the measurement with the 8-ball you have certainly altered the course of the cue ball. You may have discovered where the cue ball was, but now have no idea of where it is going (because you were measuring with the 8-ball instead of actually looking at the table).

Werner Heisenberg was the first to realize that certain pairs of measurements have an intrinsic uncertainty associated with them. For instance, if you have a very good idea of where something is located, then, to a certain degree, you must have a poor idea of how fast it is moving or in what direction. We don't notice this in everyday life because any inherent uncertainty from Heisenberg's principle is well within the acceptable accuracy we desire. For example, you may see a parked car and think you know exactly where it is and exactly how fast it is moving. But would you really know those things exactly? If you were to measure the position of the car to an accuracy of a billionth of a billionth of a centimeter, you would be trying to measure the positions of the individual atoms which make up the car, and those atoms would be jiggling around just because the temperature of the car was above absolute zero!

Heisenberg's uncertainty principle completely flies in the face of classical physics. After all, the very foundation of science is the ability to measure things accurately, and now quantum mechanics is saying that it's impossible to get those measurements exact! But the Heisenberg uncertainty principle is a fact of nature, and it would be impossible to build a measuring device which could get around it.

Spin of a particle

In 1922 Otto Stern and Walther Gerlach performed an experiment whose results could not be explained by classical physics. Their experiment indicated that atomic particles possess an intrinsic angular momentum, or spin, and that this spin is quantized (that is, it can only have certain discrete values). Spin is a completely quantum mechanical property of a particle and cannot be explained in any way by classical physics.

It is important to realize that the spin of an atomic particle is not a measure of how it is spinning! In fact, it is impossible to tell whether something as small as an electron is spinning at all! The word 'spin' is just a convenient way of talking about the intrinsic angular momentum of a particle.

Magnetic resonance imaging (MRI) uses the fact that under certain conditions the spin of hydrogen nuclei can be 'flipped' from one state to another. By measuring the location of these flips, a picture can be formed of where the hydrogen atoms (mainly as a part of water) are in a body. Since tumors tend to have a different water concentration from the surrounding tissue, they would stand out in such a picture.

What is the Schrödinger equation?

Every quantum particle is characterized by a wave function. In 1925 Erwin Schrödinger developed the differential equation which describes the evolution of those wave functions. By using Schrödinger's equation scientists can find the wave function which solves a particular problem in quantum mechanics. Unfortunately, it is usually impossible to find an exact solution to the equation, so certain assumptions are used in order to obtain an approximate answer for the particular problem.

What is a wave packet?

As mentioned earlier, the Schrödinger equation for a particular problem cannot always be solved exactly. However, when there is no force acting upon a particle its potential energy is zero and the Schrödinger equation for the particle can be exactly solved. The solution to this 'free' particle is something known as a wave packet (which initially looks just like a Gaussian bell curve). Wave packets, therefore, can provide a useful way to find approximate solutions to problems which otherwise could not be easily solved.

First, a wave packet is assumed to initially describe the particle under study. Then, when the particle encounters a force (so its potential energy is no longer zero), that force modifies the wave packet. The trick, of course, is to find accurate (and quick!) ways to 'propagate' the wave packet so that it still represents the particle at a later point in time. Finding such propagation techniques, and applying them to useful problems, is the topic of my current research.

1. Claude Cohen-Tannoudji, Bernard Diu, and Franck Laloë, Quantum Mechanics, Volumes 1 and 2, John Wiley & Sons, New York (1977).
2. John J. Brehm and William J. Mullin, Introduction to the Structure of Matter: A Course in Modern Physics, John Wiley & Sons, New York (1989).
3. Donald A. McQuarrie, Quantum Chemistry, University Science Books, Mill Valley, Calif. (1983).